Osnovna škola Jurja Habdelića Velika Gorica


| « Rujan 2024 » | ||||||
| Po | Ut | Sr | Če | Pe | Su | Ne |
| 26 | 27 | 28 | 29 | 30 | 31 | 1 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 1 | 2 | 3 | 4 | 5 | 6 |






Rad u povjerenstvu za provedbu Natjecanja iz matematike donosi razne izazove. Jedan od njih je točno i korektno bodovati zadatke na bilo kojoj razini natjecanja. To je veliki izazov jer učenici do rješenja dolaze na različite načine koja članovi povjerenstva nisu predvidjeli u „službenim“ rješenjima.
No, jedan od najvećih i najčešćih izazova je učenička žalba. Učenik koji smatra da njegovo rješenje nije korektno bodovano može uložiti žalbu na bodovanje pojedinih zadataka. ►
Učitelji i učiteljice koji rade povjerenstvu za provedbu natjecanja susreću se s raznim situacijama poput osnovanih žalbi, neosnovanih žalbi, moljakanja za bodom ili više njih pa čak i prijetnjama učenika, njihovih mentora (!) ili roditelja…
Kao dugogodišnji član povjerenstva na školskim i županijskim natjecanjima, a u zadnje dvije godine i kao član državnog povjerenstva za provedbu Natjecanja iz matematike, mišljenja sam da svakom učeniku nakon žalbenog postupka treba biti u potpunosti jasno zašto povjerenstvo jest ili nije usvojilo njegovu žalbu. Jedan od preduvjeta za razumijevanja ishoda žalbe je učeničko poznavanje načina bodovanja natjecateljskih zadataka.
Pogledajmo nekoliko primjera učeničkih rješenja natjecateljskih zadataka te kako su povjerenstva bodovala te zadatke.
 Zadani izraz ne može se zapisati u obliku potencije s brojem 2.
Zadani izraz ne može se zapisati u obliku potencije s brojem 2.
Navedena rješenja su vrlo zoran prikaz bodovanja zadataka po principu slijedi grešku.
Prvi učenik je napravio grešku u prepisivanju, izostavljajući eksponent potencije 23. Iz priloženog rješenja se vidi da učenik u potpunosti barata osnovnim računskim radnjama, redoslijedom računanja te zapisivanjem zadanog broja u obliku potencije.
Drugi učenik radi grešku pri izračunavanju zagrade. U kasnijem razgovoru s učenikom rekao je da je u brzini rješavanja zadatka umjesto zbrajanja upotrijebio množenje. Nakon označene greške učenik više nije griješio u računanju, a vidljivo je da je razmišljao i o tome da se njegovo rješenje ne može zapisati u obliku potencije s bazom 2.
Iako vrlo različite greške, a i različita rješenja, oba učenika opravdano su bodovana s većinom bodova predviđenih za taj zadatak.

Izostavljanjem uglatih zagrada učenik je promijenio uvjet zadatka i dolazi do pogrešnog rješenja. Naknadno je pogriješio pri dijeljenju brojeva –2022 i 6 (pogrešan predznak umnoška) te pri oduzimanju brojeva 2696 i 96.3. Učenik se žalio na bodovanje zadatka pozivajući se na pravilo slijedi grešku. Zbog višestrukih grešaka koje je učenik napravio, povjerenstvo nije uvažilo žalbu te je učenik bodovan s minimalnim brojem bodova.
Primjer 2.
Broj 2090 zapisan je kao umnožak šest različitih cijelih brojeva. Odredi najmanju vrijednost zbroja tih brojeva.
1. rješenje:
2090 = 2 ×5 ×11 ×19
Kako broj 2090 treba biti prikazan kao umnožak šest članova moram upotrijebiti faktore koji neće promijeniti apsolutnu vrijednost faktora. To su 1 i –1.
Umnožak parnog broja negativnih faktora je pozitivan broj.
Zbog toga što moram upotrijebiti broj 1 kao jedan od faktora najveći broj negativnih faktora je četiri.
Najmanju vrijednost zbroja faktora će biti ako su negativni faktori oni koji imaju najveću apsolutnu vrijednost: –19, –11, –5 i –1.
2090 = 1 × (–1) ×2 × (–5) ×(–11) ×(–19)
Najmanja vrijednost zbroja faktora je 1 + (–1) + 2 + (–5) + (–11) + (–19) = –33.
U ovom rješenju vidljivo je da učenik u potpunosti točno rješava zadatak objašnjavajući sve korake svojeg rješenja. Zadatak je vrednovan s maksimalnim brojem bodova.
2. rješenje:
2090 = 2 ×5 ×11 ×19
Broj 2090 treba biti prikazan kao umnožak šest članova pa su peti i šesti član broj 1 jer je on neutralan element za množenje.
Treba biti četiri negativna člana.
Najmanja vrijednost zbroja članova je –35 jer je 1 + 1 + (–2) + (–5) + (–11) + (–19) = –35.
Učenik ispravno rastavlja broj 2090 na proste faktore te shvaća da ima premalo faktora. Vidljivo je da učenik razumije koliko negativnih faktora mora upotrijebiti da bi umnožak bio pozitivan broj (iako mu tu nedostaje argumentacija zašto ne ih ne može biti dva). Nažalost, rješenje ne zadovoljava uvjet da su faktori različiti brojevi te zbog toga učenik ne dobiva točno rješenje.
U ovom rješenju je također moguće primijeniti princip slijedi grešku, ne u računskom nego u logičkom smislu zaključivanja.
Povjerenstvo je vrednovalo točne zaključke koje je učenik napisao te je zadatak bodovan s većinom bodova.
3. rješenje:
2090 = 2 ×5 ×11 ×19
Najmanja vrijednost zbroja faktora je –33.
Ovo je tipičan primjer kako se ne rješava natjecateljski zadatak. Iako je rješenje zadatka točno, nedostaje obrazloženje kako se do tog rješenja došlo. Prilikom žalbe učenik navodi da je on sve to „izračunao u glavi“. Nakon što mu je objašnjeno da u natjecateljskim zadatcima treba biti vidljiv svaki korak rješenja te da sve treba argumentirati, učenik je prihvatio obrazloženje povjerenstva. Povjerenstvo je učeniku dalo važne savjete uz nadu da mu se neće slična situacija dogoditi i narednih godina. Povjerenstvo je rješenje bodovalo sukladno predloženom načinu bodovanja.
Primjer 3.
Odredi četiri najmanja uzastopna prirodna broja takva da je prvi djeljiv s 2, drugi s 3, treću sa 7, a četvrti s 5.
1. rješenje:
Ispisujem sve višekratnike broja 7 pa ću gledati koji brojevi zadovoljavaju uvjete zadatka.
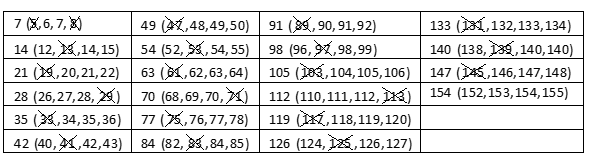 Traženi brojevi su 152, 153, 154 i 155 jer sam utvrdio niti jedna kombinacija brojeva manjih od tih brojeva ne zadovoljava uvjete zadatka.
Traženi brojevi su 152, 153, 154 i 155 jer sam utvrdio niti jedna kombinacija brojeva manjih od tih brojeva ne zadovoljava uvjete zadatka.
Navedeno rješenje je primjer rješavanja zadatka uz minimalno matematičko znanje. Učenik domišljato zaključuje da je broj 7 najveći djelitelj koji je zadan u zadatku te da će razmatrajući njegove višekratnike imati najmanje slučajeva za ispitivanje. Ispitujući slučajeve učenik propušta uočiti da ne treba promatrati sve višekratnike broja 7. Zapis koji učenik koristi je logičan, ali nije zapis koji matematičari koriste. No, učenik pokazao da je dobivena četvorka zadovoljava uvjete zadatke te je iz njegovog zapisa jasno da ne postoji četvorka manjih brojeva pa je zadatak opravdano bodovan s maksimalnim brojem bodova.
2. rješenje:
Prvi broj je djeljiv s 2 (paran je) pa završava znamenkama 0, 2, 4, 6 ili 8.
Drugi broj je djeljiv s 3 pa mu zbroj znamenaka mora biti djeljiv s 3.
Četvrti broj je djeljiv s 5 pa završava znamenkama 0 ili 5.
Ako četvrti broj završava s 0, onda prvi broj završava sa 7. To nije moguće jer je prvi broj paran.
Četvrti broj mora završavati s 5, a to znači da treći broj mora završavati sa 4.
Tražim višekratnike broja 7 koji završavaju sa 4.
To su 14, 84, 154, 224…
Ako je treći broj 14 imamo brojeve 12, 13, 14 i 15. To nije moguće jer 13 nije djeljiv s 3.
Ako je treći broj 154 imamo brojeve 152, 153, 154 i 155. Traženi brojevi zadovoljavaju uvjete zadatke.
Rješenje koje učenik navodi je logičko, zasnovano na pravilima djeljivosti prirodnih brojeva. Iako učenik odlično zaključuje rješenje zadatka nije potpuno. Učenik točno navodi da je treći član traženog niza višekratnik broja 7 koji završava znamenkom 4 te navodi koji brojevi mogu biti treći član. Nažalost, učenik ne ispituje slučaj da je treći član niza 84 te time nije pokazao da je četvorka 152, 153, 154 i 155 zaista najmanja četvorka brojeva koja zadovoljava uvjete zadatka. Povjerenstvo je zbog tog propusta učeniku oduzelo jedan bod.
3. rješenje:
Neka su rednom a, b, c i d traženi brojevi.
Broju c je zadnja znamenka 4, broju b je zadnja znamenka 3, a broju a je zadnja znamenka 2.
Broju b znamenka desetice treba biti djeljiva s 3 jer kod višekratnika broja 3 samo brojevi 03, 33, 63…sa znamenkama desetica djeljivim s 3 imaju zadnju znamenku 3.
|
1. slučaj
a = 2
b = 3
c = 4
Uvjeti nisu ispunjeni.
|
2. slučaj
a = 152
b = 153
c = 154
d= 155
|
Traženi brojevi su 152, 153, 154 i 155.
Kao i u prethodnom rješenju učenik, koristeći djeljivost prirodnih brojeva, zaključuje kojom znamenkom trebaju završavati traženi brojevi. No, učenik griješi u zaključku kako treba zapisati drugi član traženog rješenja koji je djeljiv s 3. Zaključak da je broj koji je djeljiv s 3 i koji završava znamenkom 3 nužno treba imati i znamenku desetice djeljivu s 3 je pogrešan jer vrijedi samo za dvoznamenkaste brojeve. Na primjer, broj 123 je djeljiv s 3, a ne zadovoljava učenikov uvjet. Također učenik pri ispitivanju slučajeva preskače brojeve 33, 63, 93 i 123 te ne pokazuje da je četvorka 152, 153, 154 i 155 zaista najmanja četvorka brojeva koja zadovoljava uvjete zadatka.
Nakon žalbe učenik je prihvatio obrazloženje povjerenstva i složio se da se njegovo rješenje ne može bodovati s maksimalnim brojem bodova.


Na početku zadatka učenik ispravno zaključuje da znamenka a treba biti 1, ali ne nudi objašnjenje zašto znamenka a ne može biti različita od 1. iz zapisa vidljivo je da za znamenku b zapisuje obrazloženje. Nakon određivanja znamenaka a i b učenik koristi dopuštenu metodu uzastopnog približavanja te dovršava zadatak. Učenici vrlo često u rješavanju natjecateljskih zadataka koriste metodu uzastopnog približavanja. Metoda uzastopnog približavanja korisna je ako je broj mogućnosti relativno malen. Također, za sve mogućnosti koje se metodom uzastopnog približavanja odbacuju treba obavezno zapisati argumentaciju. Zbog nedostatka argumentacije povjerenstvo je učeniku oduzelo 1 bod.
Natjecateljski zadatci predstavljaju izazov određenom dijelu učenika. Nažalost, sve manji broj učenika pristupa natjecanjima iz matematike.
Smatram sa se prije samog natjecanje učenici (a i pojedini mentori) trebaju upoznati s vrednovanjem natjecateljskih zadataka. Jedan od načina je da mentor boduje zadatak učeniku prilikom pripreme za natjecanje. Na taj način učenik ima stječe iskustvo što će mu na natjecanju biti vrednovano te može ispraviti greške koje radi u pripremama.
Posebnu važnost dao bih reviziji županijske razine natjecanja na kojoj povjerenstva ujednačavaju vrednovanje županijskih povjerenstva. Nadam se da će u skorije vrijeme sve županije prije poziva učenika na županijsku razinu natjecanja napraviti reviziju školske razine natjecanja.