Osnovna škola Jurja Habdelića Velika Gorica


| « Rujan 2024 » | ||||||
| Po | Ut | Sr | Če | Pe | Su | Ne |
| 26 | 27 | 28 | 29 | 30 | 31 | 1 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 1 | 2 | 3 | 4 | 5 | 6 |






Oduvijek su problemski zadatci bili među omiljenima tipovima zadataka kod učitelja matematike, a omraženi kod učenika. Svake godine sve više, kod osnovnoškolaca se uočavaju poteškoće u rješavanju problemskih zadataka.
Pri rješavanju problemskih zadataka većina učenika, pomalo brzopleto, pokušava postaviti pripadajući algebarski izraz bez da analizira zadatak i razmisli o uvjetima koji su u zadatku zadani. ►
Grafička metoda rješavanja problemskih zadataka jedna je od zapostavljenih metoda u nastavi matematike. U razredu, među općom populacijom učenika, odrađuje se vrlo rijetko. Nešto češće se odrađuje na dodatnoj nastavi u sklopu priprema za natjecanje.
Sljedećih nekoliko primjera pokazat će kako grafička metoda poboljšava shvaćanje problematike zadatka, olakšava njegovo razumijevanje i rješavanje.
Primjer 1.
Ante i Buga imaju zajedno 84 kuna. Ante ima 12 kuna više od Buge. Koliko novaca ima Ante, a koliko Buga.
Rješenje:
Označimo s A svotu novaca kojeg ima Ante, a s B svotu novaca kojeg ima Buga.
Svote novaca kojeg imaju Ante i Buga grafički prikazujemo pravokutnicima iste visine. Kako Ante ima više novaca pravokutnik koji prikazuje njegovu svotu novaca ima veću duljinu.
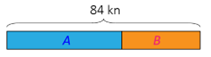
Uvjet da Ante ima 12 kuna više od Buge grafički ćemo prikazati ovako:
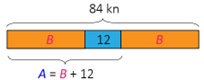
Ante ima 48 kn, a Buga 32 kn.
Primjer 2.
U voćnjaku su stabla jabuka, krušaka i šljiva. Jabuka ima dvostruko više nego krušaka, a šljiva za 10 više nego krušaka. Koliko ima stabala pojedine vrste ako je u voćnjaku ukupno 298 stabala?
Rješenje:
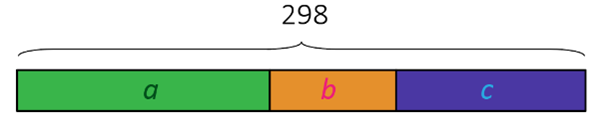
Kako je jabuka dvostruko više nego krušaka nadopunjavamo grafički prikaz.
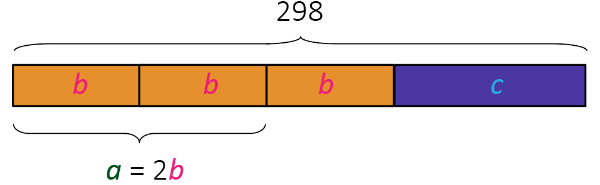
Šljiva je za 10 više od krušaka pa dobivamo završni prikaz.
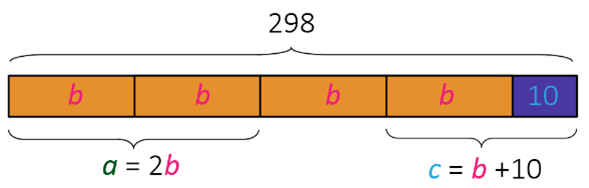
U voćnjaku je 144 stabala jabuka, 72 stabla krušaka i 82 stabla šljiva.
Za razliku do prošlih primjera gdje pri grafičkom prikazu nije bila bitna dimenzija crteža, u ovom zadatku jednostavnije ćemo napraviti grafički prikaz ako pripazimo na dimenzije.
Primjer 3.
Pješak je prešao 0.3 cijeloga puta i ostalo mu je još 21.7 km. Koliko je kilometara propješačio?
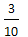 duljine puta nacrtat ćemo dužinu i podijeliti ju na 10 jednakih dijelova.
duljine puta nacrtat ćemo dužinu i podijeliti ju na 10 jednakih dijelova. 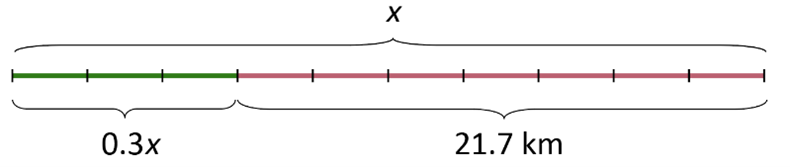
Ukupnu duljinu puta možemo sada izračunati na dva načina.
1. način
2. način
Ako je pješak propješačio 0.3 duljine puta, onda nije propješačio 0.7 duljine puta (jer je 1 – 0.3 = 0.7).
Duljina puta koju nije propješačio iznosi 21.7 km pa vrijedi
Ukupan put je dug 31 km pa je pješak propješačio 31 – 21.7 = 9.3 km.
Učenicima često probleme zadaju zadatci u kojima se zadanim skupovima članovi dodaju ili uklanjaju te ako se neki članovi jednog skupa postanu članovi drugog skupa.
Primjenom grafičke metode kod takvih zadataka vidno se pojačava razumijevanje problema.
Evo nekoliko takvih primjera zadataka.
Primjer 4.
Na jednom (prvom) brodu bilo je 2 puta više turista nego na drugome. Kad je u luci s prvog broda sišlo 98 turista, a s drugoga 16, na svakom je brodu ostao jednak broj turista. Koliko je turista bilo na početku na svakom brodu?
Rješenje:
Označimo s x broj turista na drugom brodu. Po uvjetu zadatka broj turista na drugom brodu označimo s 2x.
Grafički prikaz broja turista na brodovima prije dolaska u luku je:
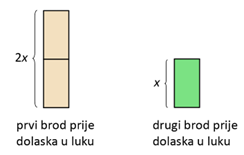
Iskrcaj određenog broja putnika iz brodova grafički prikazujemo ovako:
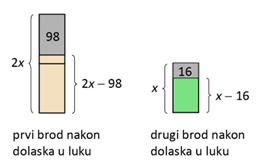
Po uvjetu zadatka nakon iskrcaja putnika na oba broda preostao je jednak broj putnika pa imamo jednakost:
Zaključujemo da je na prvom brodu bilo 2 × 82 = 164 putnika, a na drugom 82 putnika.
Primjer 5.
U dva jata ima 27 golubova. Ako iz prvog jata 3 goluba prelete u drugo, tada će biti 2 puta više golubova u drugom jatu nego što ih je ostalo u prvome. Koliko je bilo golubova u svakom jatu na početku?
Rješenje:
Označimo li s x broj golubova u prvom jatu, onda je u drugome jatu ostatak golubova, tj. u drugom jatu ima 27 – x golubova.
Grafički ćemo to prikazati na sljedeći način (uz napomenu da prebrojavanjem broja nacrtanih ptica u grafičkom prikazu ne dolazimo do točnog rješenja).
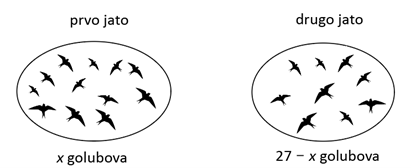
Kada iz prvog jata u drugo prelete tri goluba onda će se broj golubova u prvom jatu umanjiti za 3, a broj golubova u drugom jatu uvećati za 3. Grafički to možemo prikazati ovako:
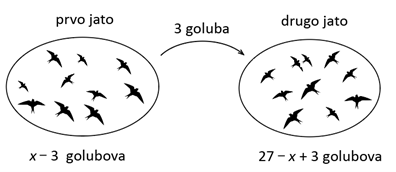
Nakon preleta u drugom jatu ima dva puta više golubova. To znači da ćemo broj golubova iz prvog jata udvostručiti da bismo dobili broj golubova u drugom jatu. Dobivamo sljedeću jednakost:
U prvom jatu je bilo 12 golubova, a u drugom 27 – 12 = 15 golubova.
Grafička metoda rješavanje problemskih zadataka dolazi do izražaja u zadatcima vezanim za jednoliko gibanje. Iako takvi zadatci pripadaju više fizici nego matematici, mogu se riješiti i u nižim razredima osnovne škole.
Primjer 6.
Iz dvaju gradova, među kojima je udaljenost 250 kilometara, istodobno krenu jedan drugome ususret dva motociklista. Nakon dva sata vožnje do susreta ima još 30 kilometara. Brzina jednoga veća je 10 kilometara na sat od brzine drugoga. Kojom se brzinom kreće svaki motociklist?
Rješenje:
Prvi motociklist u jednom satu prijeđe put duljine s km, a drugi motociklist duljine s + 10 km (jer je njegova brzina za 10 km na sat veća od prvog motociklista).
Grafički to prikazujemo ovako:
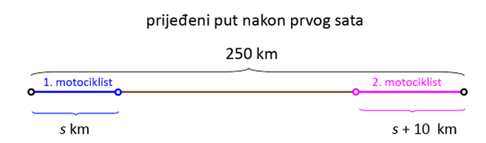
U dva sata prvi motociklist prijeđe put duljine 2s km, a drugi motociklist duljine 2(s + 10) km.
Grafički to prikazujemo ovako:
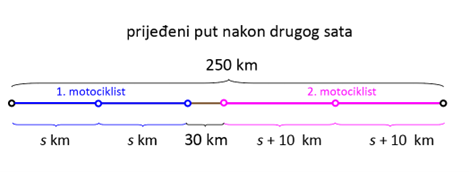
Zbroj prijeđenih udaljenosti prvog i drugog motociklista i udaljenosti među njima jednak je udaljenosti gradova. Stoga imamo jednakost:
Prvi motociklist u jednom satu napravi 50 km pa je njegova brzina 50 km/h. Drugi motociklist u jednom satu napravi 10 km više od prvog motociklista tj. 60 km pa je njegova brzina 60 km/h.
I za kraj jedan zadatak s školske/gradske razine natjecanja za 7. razred.
Primjer 7.
Ubrano je 600 kg gljiva čija je vlažnost 98 %. Nakon sušenja vlažnost je smanjena na 96 %. Kolika je masa gljiva nakon sušenja?
Rješenje:
Kako je vlažnost gljiva 98 % znači da gljive sadržavaju 2 % suhe tvari.
Kako je 2 % od 600 je 12. Dakle, masa suhe tvari u gljivama je 12 kg, a masa vode 588 kg.
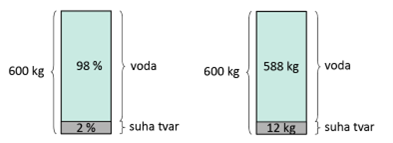
Sušenjem gljiva udio vode se smanjio na 96 %, a udio suhe tvari povećao na 4 %. Kako se sušenjem masa suhe tvari ne smanjuje, masa suhe tvari je i dalje 12 kg.
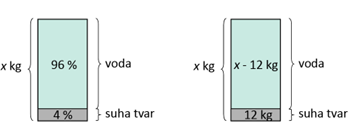
Dakle, zadatak ćemo riješiti tako da izračunamo od kojeg broja je 4 % jednako 12.
Masa gljiva nakon sušenja je 300 kg.
Iako naš mozak najveći dio informacija prikuplja vizualnim putem problem vizualizacije problemskih zadataka je jedan od većih problema u nastavi matematike.
Pri rješavanju problemskih zadataka prednost dobiva algebarska metoda koja se, kod nekih učenika, u zahtjevnijim zadatcima pokazuje nedostatna.
Grafička metoda rješavanja zadataka učenicima približava problematiku zadatka jer učenici „mogu vidjeti“ što se u zadatku traži.
Učenicima je potrebno vrijeme za privikavanje rješavanja problemskih zadataka grafičkom metodom. U želji da što brže riješe zadatak, preskaču jednostavnije zadatke riješiti grafičkom metodom pa im nedostaje temeljnog iskustva kako riješiti složenije zadatke.
Iskustvo u radu s učenicima pokazuje da se kombinacijom algebarske i grafičke metode rješavanja problemskih zadataka postižu bolji rezultati te da učenici razvijaju vizualizaciju i logičko razmišljanje.
Literatura: